MySQL索引

索引是什么？

索引是为了加速对表中数据行的检索而创建的一种分散存储的 数据结构。

首先数据是以文件的形式存放在磁盘上面的，每一行数据都有它的磁盘地址。如果 没有索引的话，要从 500 万行数据里面检索一条数据，只能依次遍历这张表的全部数据，直到找到这条数据。

但是有了索引之后，只需要在索引里面去检索这条数据就行了，因为它是一种特殊 的专门用来快速检索的数据结构，我们找到数据存放的磁盘地址以后，就可以拿到数据 了。

索引类型

• 普通索引也叫非唯一索引，是最普通的索引，没有任何的限制。
• 唯一索引唯一索引要求键值不能重复。另外需要注意的是，主键索引是一 种特殊的唯一索引，它还多了一个限制条件，要求键值不能为空。主键索引用 primay key 创建。
• 全文索引针对比较大的数据，比如我们存放的是消息内容，有几 KB 的数 据的这种情况，如果要解决 like 查询效率低的问题，可以创建全文索引。只有文本类型 的字段才可以创建全文索引，比如 char、varchar、text。

为什么使用B+树，索引数据结构演进过程

二分查找

有序数组的等值查询和比较查询效率非常高，但是更新数据的时候会出现一个问题， 可能要挪动大量的数据(改变 index)，所以只适合存储静态的数据。

为了支持频繁的修改，比如插入数据，我们需要采用链表。链表的话，如果是单链 表，它的查找效率还是不够高。

有没有可以使用二分查找的链表呢?

二叉查找树(BST Binary Search Tree)

左子树所有的节点都小于父节点，右子树所有的节点都大于父节点。投影到平面以 后，就是一个有序的线性表。

二叉查找树既能够实现快速查找，又能够实现快速插入。

存在的问题：

就是它的查找耗时是和这棵树的深度相关的，在最坏的情况下时间复杂度会退化成
O(n)。

动态演示二叉查找数

如果插入的数据是一个有序的

它会变成链表(我们把这种树叫做“斜树”)，这种情况下不能达到加快检索速度 的目的，和顺序查找效率是没有区别的。

因为左右子树深度差太大，这棵树的左子树根本没有节点——也就是它不够平衡。 所以，我们有没有左右子树深度相差不是那么大，更加平衡的树呢?

平衡二叉树 (左旋转，右旋转)

平衡二叉树的定义:左右子树深度差绝对值不能超过 1。

所以为了保持平衡，AVL 树在插入和更新数据的时候执行了一系列的计算和调整的

平衡二叉树动态演示

平衡二叉树作为索引怎么查询数据?

第一个是索引的键值。比如我们在 id 上面创建了一个索引，我在用 where id =1 的 条件查询的时候就会找到索引里面的 id 的这个键值。

第二个是数据的磁盘地址，因为索引的作用就是去查找数据的存放的地址。

第三个，因为是二叉树，它必须还要有左子节点和右子节点的引用，这样我们才能 找到下一个节点。比如大于 26 的时候，走右边，到下一个树的节点，继续判断。

如果是这样存储数据的话，我们来看一下会有什么问题。

我们用树的结构来存储索引的时候，访问一个节点就要跟磁盘之间发生一次 IO。 InnoDB 操作磁盘的最小的单位是一页(或者叫一个磁盘块)，大小是 16K(16384 字节)。

那么，一个树的节点就是 16K 的大小。

如果我们一个节点只存一个键值+数据+引用，例如整形的字段，可能只用了十几个 或者几十个字节，它远远达不到 16K 的容量，所以访问一个树节点，进行一次 IO 的时候， 浪费了大量的空间。

所以如果每个节点存储的数据太少，从索引中找到我们需要的数据，就要访问更多 的节点，意味着跟磁盘交互次数就会过多。

数据越多，树深度越深，磁盘交互次数越多。

所以我们的解决方案是什么呢?

第一个就是让每个节点存储更多的数据。

第二个，节点上的关键字的数量越多，我们的指针数也越多，也就是意味着可以有更多的分叉(我们把它叫做“路数”)。

因为分叉数越多，树的深度就会减少(根节点是 0)。

这样，我们的树是不是从原来的高瘦高瘦的样子，变成了矮胖矮胖的样子?

这个时候，我们的树就不再是二叉了，而是多叉，或者叫做多路。

多路平衡查找树(B Tree)(分裂、合并)

这个就是我们的多路平衡查找树，叫做 B Tree(B 代表平衡)。

动态演示地址

比如 Max Degree(路数)是 3 的时候，我们插入数据 1、2、3，在插入 3 的时候， 本来应该在第一个磁盘块，但是如果一个节点有三个关键字的时候，意味着有 4 个指针， 子节点会变成 4 路，所以这个时候必须进行分裂。把中间的数据 2 提上去，把 1 和 3 变 成 2 的子节点。

如果删除节点，会有相反的合并的操作。

注意这里是分裂和合并，跟 AVL 树的左旋和右旋是不一样的。

我们继续插入 4 和 5，B Tree 又会出现分裂和合并的操作。

从这个里面我们也能看到，在更新索引的时候会有大量的索引的结构的调整，所以 解释了为什么我们不要在频繁更新的列上建索引，或者为什么不要更新主键。

节点的分裂和合并，其实就是 InnoDB 页的分裂和合并。

B+树(加强版多路平衡查找树)

B Tree 的效率已经很高了，为什么 MySQL 还要对 B Tree 进行改良，最终使用了 B+Tree 呢?

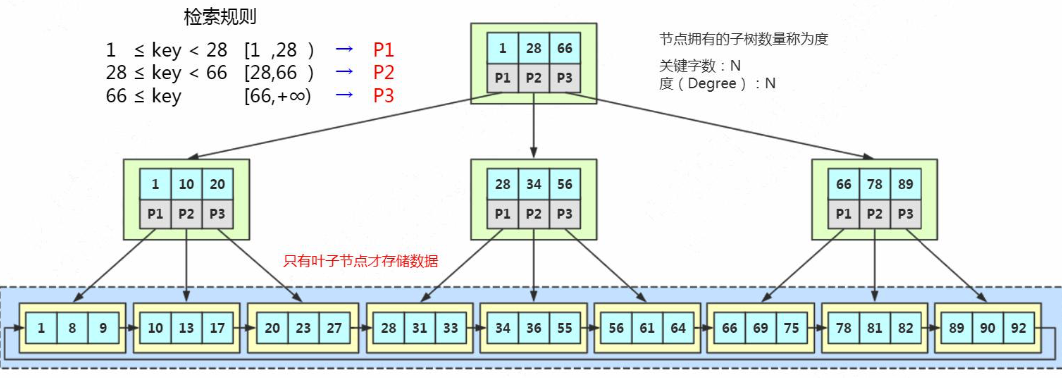
MySQL 中的 B+Tree 有几个特点:

• 它的关键字的数量是跟路数相等的;
• B+Tree 的根节点和枝节点中都不会存储数据，只有叶子节点才存储数据。搜索到关键字不会直接返回，会到最后一层的叶子节点。比如我们搜索 id=28，虽然在第一 层直接命中了，但是全部的数据在叶子节点上面，所以我还要继续往下搜索，一直到叶子节点。
• B+Tree 的每个叶子节点增加了一个指向相邻叶子节点的指针，它的最后一个数 据会指向下一个叶子节点的第一个数据，形成了一个有序链表的结构。
• 它是根据左闭右开的区间 [ )来检索数据。

B+Tree 的数据搜寻过程:

1. 比如我们要查找 28，在根节点就找到了键值，但是因为它不是页子节点，所以 会继续往下搜寻，28 是[28,66)的左闭右开的区间的临界值，所以会走中间的子节点，然 后继续搜索，它又是[28,34)的左闭右开的区间的临界值，所以会走左边的子节点，最后 在叶子节点上找到了需要的数据。

2. 第二个，如果是范围查询，比如要查询从 22 到 60 的数据，当找到 22 之后，只 需要顺着节点和指针顺序遍历就可以一次性访问到所有的数据节点，这样就极大地提高了区间查询效率(不需要返回上层父节点重复遍历查找)。

InnoDB 中的 B+Tree 的特点:

1. 它是 B Tree 的变种，B Tree 能解决的问题，它都能解决。B Tree 解决的两大问题 是什么?(每个节点存储更多关键字;路数更多)
2. 扫库、扫表能力更强(如果我们要对表进行全表扫描，只需要遍历叶子节点就可以 了，不需要遍历整棵 B+Tree 拿到所有的数据)
3. B+Tree 的磁盘读写能力相对于 B Tree 来说更强(根节点和枝节点不保存数据区， 所以一个节点可以保存更多的关键字，一次磁盘加载的关键字更多)
4. 排序能力更强(因为叶子节点上有下一个数据区的指针，数据形成了链表) 5)效率更加稳定(B+Tree 永远是在叶子节点拿到数据，所以 IO 次数是稳定的)

为什么不用红黑树?

• 只有两路;
• 不够平衡。

索引方式:真的是用的 B+Tree 吗?

创建索引，索引方式有两种。

• Hash ：以 KV 的形式检索数据，也就是说，它会根据索引字段生成哈希码和指针， 指针指向数据。

  1. 它的时间复杂度是 O(1)，查询速度比较快。因为哈希索引里面的数据不是 按顺序存储的，所以不能用于排序。

2. 我们在查询数据的时候要根据键值计算哈希码，所以它只能支持等值查询 (= IN)，不支持范围查询(> < >= <= between and)

3. 如果字段重复值很多的时候，会出现大量的哈希冲突(采用拉链法解 决)，效率会降低。

• B+Tree。

索引使用原则

• 列的离散(sàn)度

  如果列的重复值越多，离散度就越低，重复值越少，离散度就越高

• 联合索引最左匹配

• 覆盖索引

  非主键索引，我们先通过索引找到主键索引的键值，再通过主键值查出索引里面没 有的数据，它比基于主键索引的查询多扫描了一棵索引树，这个过程就叫回表。

  在辅助索引里面，不管是单列索引还是联合索引，如果 select 的数据列只用从索引 中就能够取得，不必从数据区中读取，这时候使用的索引就叫做覆盖索引，这样就避免 了回表。

索引的创建与使用

• 在用于 where 判断 order 排序和 join 的(on)字段上创建索引
• 索引的个数不要过多。——浪费空间，更新变慢。
• 区分度低的字段，例如性别，不要建索引。——离散度太低，导致扫描行数过多。
• 频繁更新的值，不要作为主键或者索引。——页分裂
• 组合索引把散列性高(区分度高)的值放在前面。
• 创建复合索引，而不是修改单列索引。
• 过长的字段如何建立索引？

  前缀索引，并不是一个万能药，他的确可以帮助我们对一个写过长的字段上建立索引。但也会导致排序（order by ，group by）查询上都是无法使用前缀索引的。

• 为什么不建议用无序的值(例如身份证、UUID )作为索引?

  新行的值不一定要比之前的主键的值要大,所以innodb无法做到总是把新行插入到索引的最后,而是需要为新行寻找新的合适的位置从而来分配新的空间。这个过程需要做很多额外的操作，数据的毫无顺序会导致数据分布散乱
  写入的目标页很可能已经刷新到磁盘上并且从缓存上移除，或者还没有被加载到缓存中，innodb在插入之前不得不先找到并从磁盘读取目标页到内存中，这将导致大量的随机IO
  因为写入是乱序的,innodb不得不频繁的做页分裂操作,以便为新的行分配空间,页分裂导致移动大量的数据，一次插入最少需要修改三个页以上
  由于频繁的页分裂，页会变得稀疏并被不规则的填充，最终会导致数据会有碎片

什么时候用不到索引?

• 索引列上使用函数(replace\SUBSTR\CONCAT\sum count avg)、表达式、 计算(+ - * /)

• 字符串不加引号，出现隐式转换

• like 条件中前面带%

• 负向查询

  NOT LIKE不可以

  != (<>)和 NOT IN 在某些情况下可以

聚簇索引与非聚簇索引

• 聚簇索引：将数据存储与索引放到了一块，找到索引也就找到了数据
• 非聚簇索引：将数据存储于索引分开结构，索引结构的叶子节点指向了数据的对应行，myisam通过key_buffer把索引先缓存到内存中，当需要访问数据时（通过索引访问数据），在内存中直接搜索索引，然后通过索引找到磁盘相应数据，这也就是为什么索引不在key buffer命中时，速度慢的原因

由于聚簇索引是将数据跟索引结构放到一块，因此一个表仅有一个聚簇索引